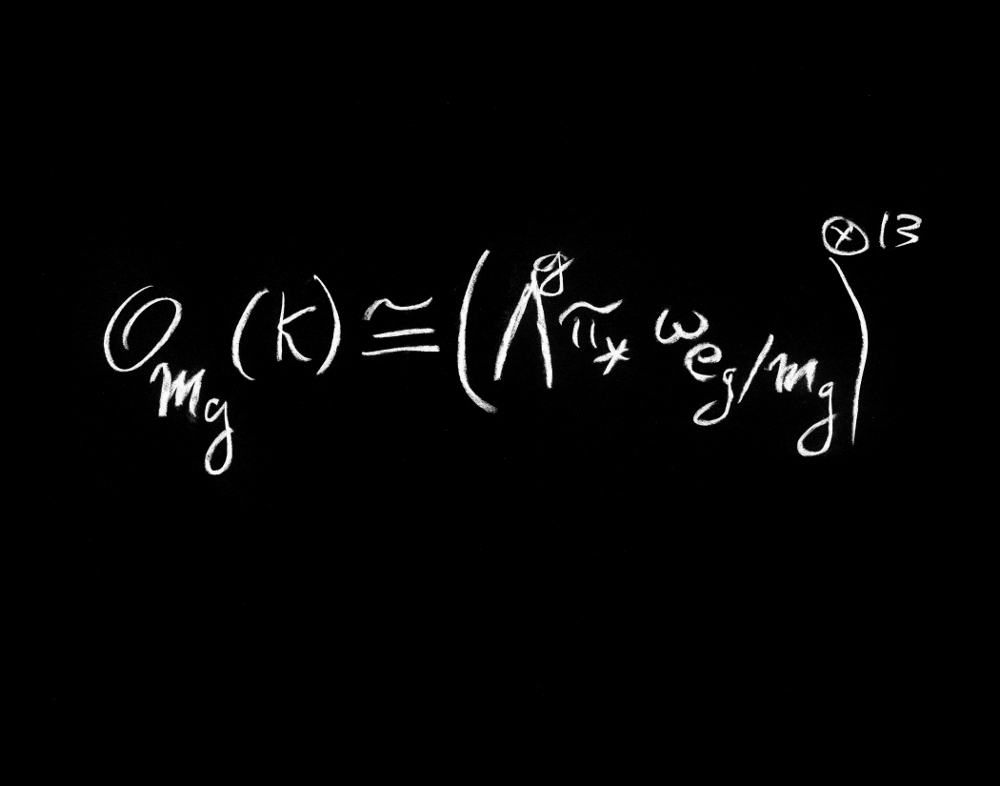Thirteen??
David Mumford
A large part of what a mathematician does may be described as exploring "things" which they discover through reasoning, which become as real to them as the house they live in but which have no material existence at all. Some easy examples are the higher-dimensional analogs of the Platonic solids. One of the spires on Gaudi's Sagrada Familia is expected to have an icosahedron on it -- the twenty-sided regular polyhedron. This is a real tangible thing. But mathematicians all feel space can have more than three dimensions and in the 19th century Schläfli discovered some marvelous four-dimensional versions of Plato's list that we can only imagine. My own passion for a long time focused on the things written as Mg in my formula, known as the "moduli space of curves of genus g". Even by a mathematician's standards for reality, when I was a student these spaces seemed shrouded in fog, in a limbo between full-fledged mathematical existence and fantasy. I wanted to change that.
At that time, Alexander Grothendieck burst on the scene. A truly unique person, he had the skill of passing to higher levels of abstraction than anyone before and using these abstractions to shine a brilliant light on relatively concrete things we didn't yet understand. It turned out that one of his deep results could be applied to my still dimly perceived space. I didn't know then what to make of this. The power of the result only became apparent some twenty years later working with Joe Harris, when we knew enough to be able to treat Mg as a real object (technically, a quasi-projective algebraic variety).
So what is the formula about and why is it beautiful? It states that two things ("line bundles") are essentially the same ("isomorphic"). The one on the left is the key object that determines the geometry of any space like Mg. Going back to Gauss, we have known that in crudest terms there are three kinds of spaces: flat ones like a plane, positively curved ones like the surface of the earth and negatively curved ones like the surface of a saddle (where the sum of the angles of a triangle is less than 180°). The object on the left controls where our space sits in this tripartite categorization. The object on the right is what Raoul Bott called a "tautological" structure: a basic decoration produced by the very definition of the space Mg. Their isomorphism turned out to be the key that showed these spaces belong to the negative category if g is large enough.
The most startling thing about the formula is the number thirteen. You can look in many math journals and find that the only numbers greater than two are the page numbers. This thirteen has a pedigree in a long tradition of counting things, e.g. that a cubic surface has exactly 27 straight lines on it (including complex ones!) but, frankly, it still feels to me like a strange joke the creator is playing on us.